Notice
Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 백준
- 스프링
- TIL
- database
- Git
- 알고리즘
- Oracle
- flask
- 데이터베이스
- PYTHON
- mybatis
- 플라스크
- 링크
- java
- 이클립스
- 자바스크립트
- javascript
- jQuery
- eclipse
- db
- sql
- 오라클
- 자바
- spring
- 웹프로그래밍
- mysql
- 에러
- 파이썬
- rdbms
- BOJ
Archives
- Today
- Total
기록과 정리의 공간
[알고리즘] 백준 11053번 : 가장 긴 증가하는 부분 수열 본문
백준 11053번 : 가장 긴 증가하는 부분 수열(문제 링크)
- 사용 언어 : 파이썬(Python)
- 문제 유형 : 동적 프로그래밍(DP), LIS
- 난이도 : 하
소스코드
import sys
n = int(sys.stdin.readline())
array = list(map(int, sys.stdin.readline().split()))
D = [1] * n
for i in range(1, n):
for j in range(0, i):
if array[j] < array[i]:
D[i] = max(D[i], D[j] + 1)
print(max(D))설명
- 가장 긴 증가하는 부분 수열(LIS) 문제는 전형적인 DP문제이다.(반드시 알아두기!)
- 수열의 크기가 n일 떄, 기본적인 DP알고리즘으로 O(n^2)에 해결 가능하다.
- 우선적으로, 이 문제에 대한 점화식은 다음과 같다. 이 점화식을 그대로 코드로 옮기면 된다.
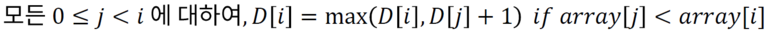
- D[i]는 array[i]를 마지막 원소로 가지는 부분 수열의 최대 길이를 의미한다.
- 문제 링크의 예시 데이터와 점화식을 바탕으로 for반복문이 실행되는 동안 갱신되는 리스트 D의 값들을 표로 나타내보면 다음과 같다.
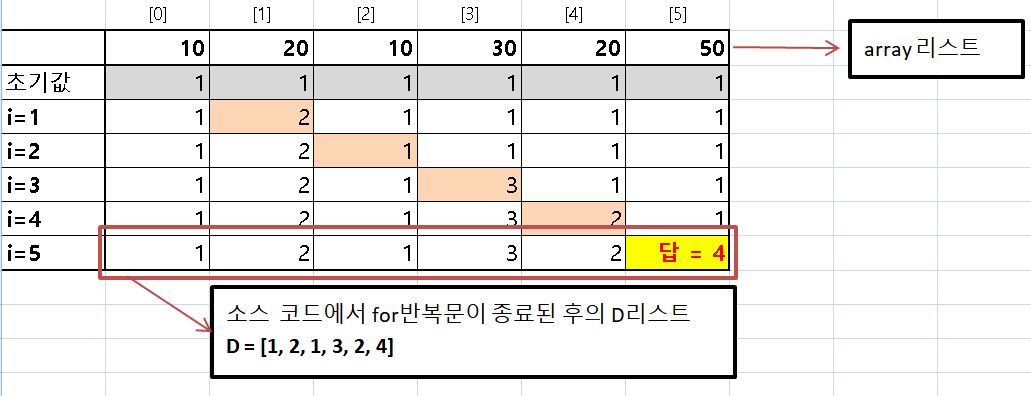
- 2번 째 행의 초기값은 전부 1이다. 이는 자기 자신만을 원소로 가지는 부분 수열이 길이를 의미힌다.
- i=1 일 때, j의 범위는 0 뿐이다. 이 때, array[0] < array[1] 이므로, D[1] = max(D[1], D[0] + 1) = max(1, 1+1) = 2 가 된다.
이는 D[1], 즉 array[1] = 20을 마지막 원소로 하는 부분 수열은 {10, 20}으로 최대 길이가 2라는 것을 의미힌다. - i=3 일 때, j의 범위는 0, 1, 2 가 되는데, array[0], array[1], array[2] 전부 array[3]보다 작은 값이므로, D[3] = max(D[3], D[0]+1) = (1, 2) = 2, D[3] = max(D[3], D[1]+1) = (2, 3) = 3, D[3] = max(D[3], D[2] + 1) = (3, 2) = 3 에서 최종적으로 3이 된다.
이는 D[3], 즉 array[3] = 30을 마지막 원소로 하는 부분 수열은 {10, 20, 30}으로 최대 길이가 3이라는 것을 의미힌다. - 나머지도 경우도 위와 같은 방식으로 진행 된다.
- for반복문이 종료된 후, D = [1, 2, 1, 3, 2, 4] 가 되고 이 중 가장 큰 값인 4가 정답이 된다.
'문제풀이 > 백준(BOJ)' 카테고리의 다른 글
| [알고리즘] 백준 9251번 : LCS (0) | 2020.08.08 |
|---|---|
| [알고리즘] 백준 12865번 : 평범한 배낭 (0) | 2020.08.06 |
| [알고리즘] 백준 1904번 : 01타일 (0) | 2020.08.05 |
| [알고리즘] 백준 1766번 : 문제집 (0) | 2020.08.05 |
| [알고리즘] 백준 1991번 : 트리 순회 (0) | 2020.07.17 |
Comments




